Stokes' law
(From Wikipedia)
Not to be confused with Stokes' theorem.

Creeping flow past a sphere: streamlines, drag force Fd and force by gravity Fg.
- Fd is the frictional force acting on the interface between the fluid and the particle (in N),
- μ is the dynamic viscosity (N s/m2),
- R is the radius of the spherical object (in m), and
- vs is the particle's settling velocity (in m/s).
- vs is the particles' settling velocity (m/s) (vertically downwards if ρp > ρf, upwards if ρp < ρf ),
- g is the gravitational acceleration (m/s2),
- ρp is the mass density of the particles (kg/m3), and
- ρf is the mass density of the fluid (kg/m3).
- Laminar Flow
- Spherical particles
- Homogeneous (uniform in composition) material
- Smooth surfaces
- Particles do not interfere with each other
The CGS unit of kinematic viscosity was named "stokes" after his work.
Flow visualization:


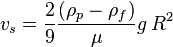
No comments:
Post a Comment